背包问题及其优化
发表更新算法26 分钟读完 (大约3887个字)0次访问

背包问题及其优化

详细总结了01背包问题、完全背包问题、多重背包问题、分组背包问题以及混合背包问题的DP解法及其优化。

01背包问题

问题描述

01背包问题的描述如下：

有$N$件物品和一个容量是$V$的背包。

每件物品只能使用一次。第$i$件物品的体积是$v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式：

第一行两个整数$N$，$V$，用空格隔开，分别表示物品数量和背包容积。

接下来有$N$行，每行两个整数$v_i$，$w_i$，用空格隔开，分别表示第$i$件物品的体积和价值。

输出格式：

输出一个整数，表示最大价值。

数据范围：

输入样例：

1
2
3
4
5
4 5
1 2
2 4
3 4
4 5

输出样例：

1
8

问题分析

画出思维导图如下：

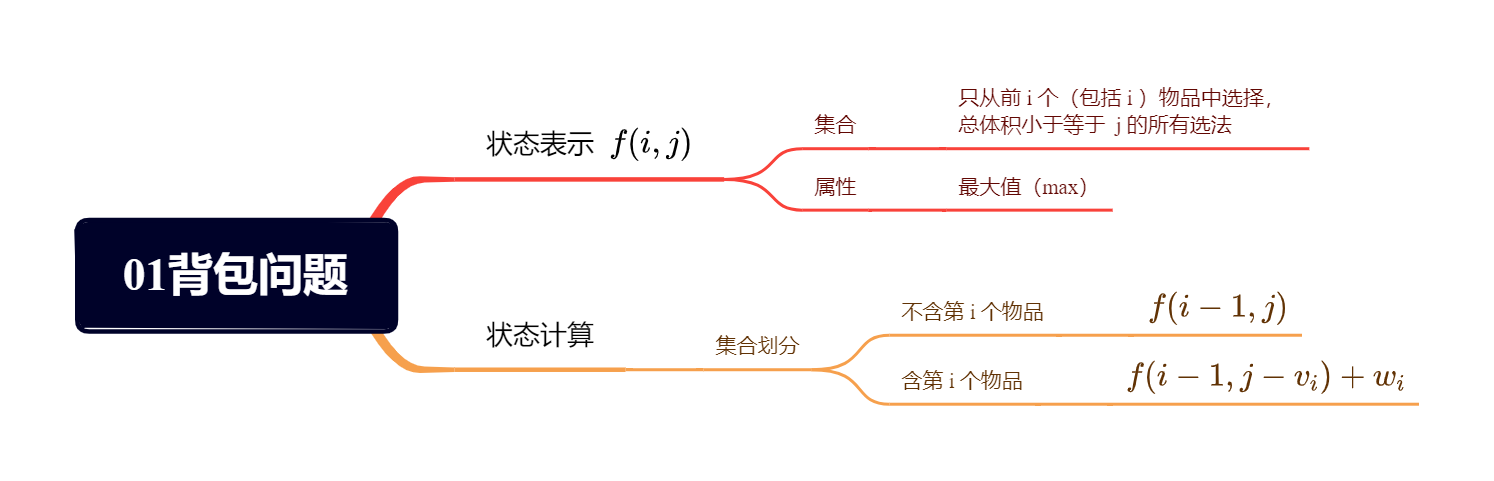
01背包问题

状态转移方程为，

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;
const int N = 1010, M = 1010;
int n, m, v[N], w[N];
int f[N][M];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++)
        scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    
    printf("%d", f[n][m]);
    return 0;
        
}
  • 时间复杂度：$O(NV)$
  • 空间复杂度：$O(NV)$

代码优化

优化一

观察到每次迭代，第$i$层都会将第$i-1$层覆盖，考虑使用滚动数组进行实现，减小存储空间的使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N = 1010, M = 1010;
int v[N], w[N];
int f[M];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j --) // 由于f[i - 1][j - v[i]]使用的是上一层的值，故此处应该从大到小更新，防止将上一层的值覆盖
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    printf("%d", f[m]);
    return 0;
}

  • 时间复杂度：$O(NV)$
  • 空间复杂度：$O(V)$

优化二

在优化一的基础上，可以一边输入一边计算，减少使用的存储空间：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
using namespace std;

const int N = 1010, M = 1010;
int n, m;
int f[M];

int main() {
    cin >> n >> m;
    int v, w;
    for (int i = 0; i < n; i ++) {
        cin >> v >> w;
        for (int j = m; j >= v; j --)
            f[j] = max(f[j], f[j - v] + w);
    }
    cout << f[m] << endl;
    return 0;
}
  • 时间复杂度：$O(NV)$
  • 空间复杂度：$O(V)$

完全背包问题

问题描述

完全背包问题的描述如下：

有$N$种物品和一个容量是$V$的背包。

每种物品都有无限个可用。第$i$种物品的体积是$v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式：

第一行两个整数$N$，$V$，用空格隔开，分别表示物品数量和背包容积。

接下来有$N$行，每行两个整数$v_i$，$w_i$，用空格隔开，分别表示第$i$件物品的体积和价值。

输出格式：

输出一个整数，表示最大价值。

数据范围：

输入样例：

1
2
3
4
5
4 5
1 2
2 4
3 4
4 5

输出样例：

1
10

问题分析

画出思维导图如下：

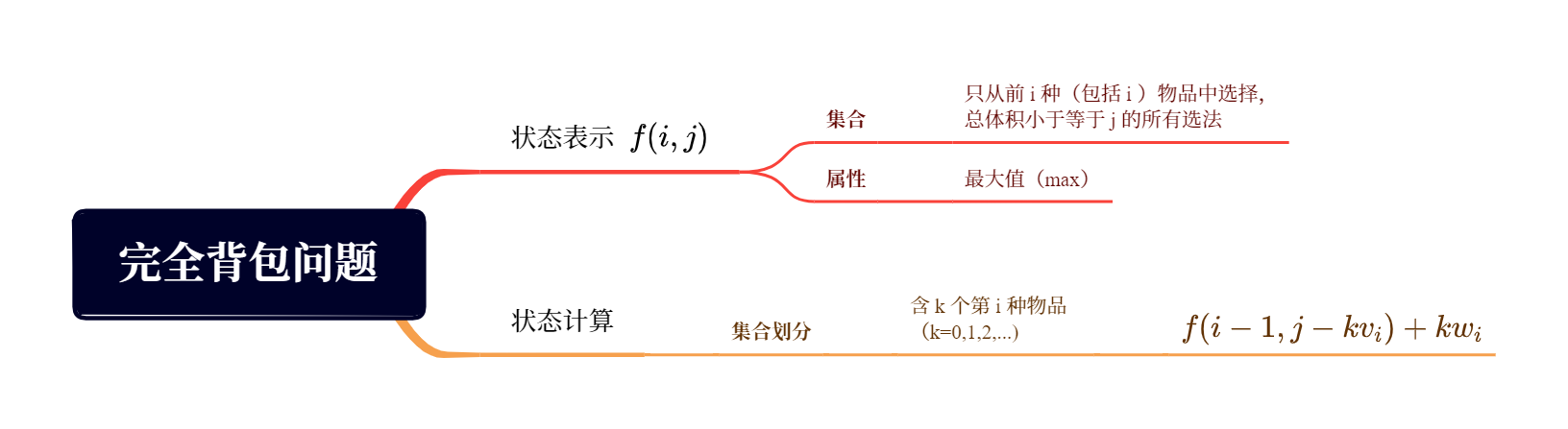
完全背包问题

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N], v[N], w[N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++)
            for (int k = 0; k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);

    printf("%d", f[n][m]);
    return 0;
}

当$v_i$都为1时，最坏情况下时间复杂度为：$O(NVv^2)$。

代码优化

时间优化

观察到，

即$f(i, j-v_i)+w_i$与$f(i,j)$第二项开始的项相等。因此有，

优化后的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N], v[N], w[N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
            

    printf("%d", f[n][m]);
    return 0;
}

  • 时间复杂度：$O(NV)$
  • 空间复杂度：$O(NV)$

空间优化

优化一

与01背包类似，减小一维数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i ++)
        for (int j = v[i]; j <= m; j ++) // 由于f[i][j - v[i]]使用的是当前层的值，故此处应该从小到大更新，防止使用上一层的值
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    printf("%d", f[m]);
    return 0;
}

  • 时间复杂度：$O(NV)$

  • 空间复杂度：$O(V)$

    优化后的代码与01背包的区别在于，完全背包的第二层循环是从小到大更新，而01背包为从大到小更新。

优化二

在优化一的基础上，边输入边计算，减小代码量与存储空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
using namespace std;

const int N = 1010, M = 1010;
int n, m;
int f[M];

int main() {
    cin >> n >> m;
    int v, w;
    for (int i = 0; i < n; i ++) {
        cin >> v >> w;
        for (int j = v; j <= m; j ++)
            f[j] = max(f[j], f[j - v] + w);
    }
    cout << f[m] << endl;
    return 0;
}

  • 时间复杂度：$O(NV)$

  • 空间复杂度：$O(V)$

多重背包问题

问题描述

多重背包问题的描述如下：

有$N$件物品和一个容量是$V$的背包。

第$i$种物品最多有$s_i$件，每件体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式：

第一行两个整数$N$，$V$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行两个整数$v_i$，$w_i$，$s_i$，用空格隔开，分别表示第$i$件物品的体积、价值和数量。

输出格式：

输出一个整数，表示最大价值。
数据范围一（无需优化）：

数据范围二（需要二进制优化）：

输入样例：

1
2
3
4
5
4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

1
10

问题分析

多重背包问题与完全背包问题分析过程类似，思维导图如下：

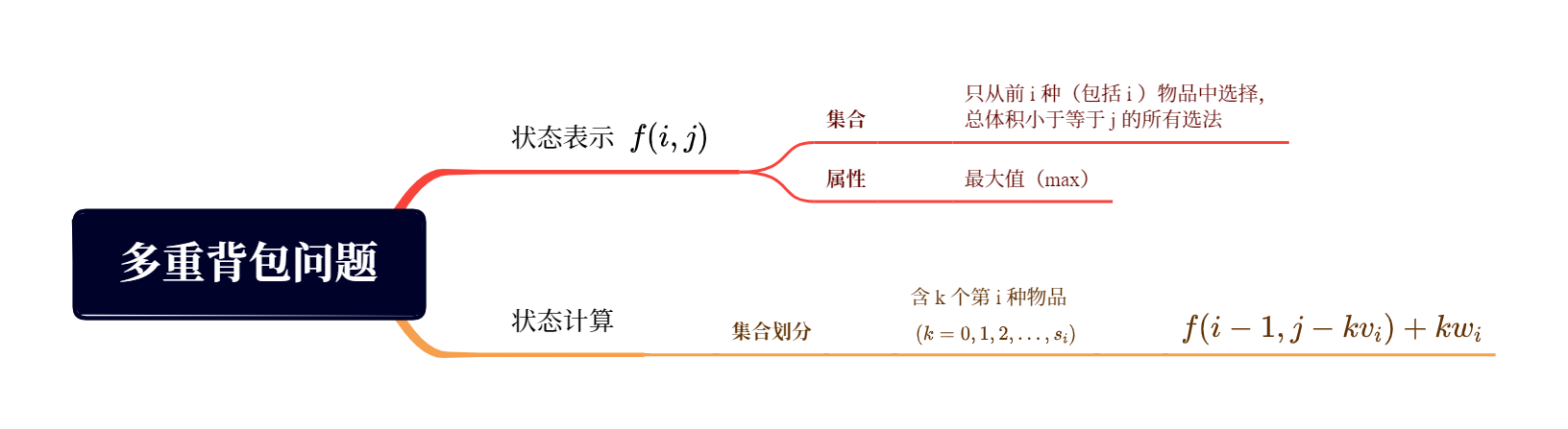
多重背包问题

状态转移方程为：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N = 110;
int f[N][N], v[N], w[N], s[N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
    
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++)
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    
    printf("%d", f[n][m]);
    return 0;
}
  • 当$s$都为$N$，且$v_i$都为1时，最坏时间复杂度：$O(NV^2)$
  • 空间复杂度：$O(NV)$

代码优化

优化一

当$N$和$V$，以及$v_i,w_i,s_i$较大时，上述代码时间复杂度较高，会造成超时（在C++中，每秒大约计算$10^8$次），因此考虑对其进行优化。

类似的，由完全背包问题可以得到，

观察得到该式子比原状态转移方程多一项，即$f(i - 1, j - (s_i+1)v_i) + s_iw_i)$，因此不能使用优化完全背包的方法来优化多重背包问题，只能另辟蹊径。

使用二进制优化，将每种物品进行打包，然后使用01背包的方法进行解决。例如， 若某种物品有200件，将其分别打包成1, 2, 4, 8, 16, 32, 64, 73共8件，由于1~200之间的每个数都可以用这8件打包的物品数量凑出，将每一件打包的物品视作01背包问题中的一类物品，即可使用01背包进行解决。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
using namespace std;
const int N = 22000;	// N * V * log(s)
int f[N], v[N], w[N];

int main()
{
    int n, m;
    cin >> n >> m;
    int a, b, s, cnt = 0;
    for (int i = 0; i < n; i ++)
    {
        scanf("%d%d%d", &a, &b, &s);
        int k = 1;
        while (k <= s)
        {
            cnt ++;
            v[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if (s)
        {
            cnt ++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }
    }
    n = cnt;
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    printf("%d", f[m]);
    return 0;
}
  • 时间复杂度为：$O(NV)$
  • 空间复杂度为：$O(V)$

优化二

在优化一的基础上，边输入边计算，减小代码量和存储空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;

const int N = 1010, M = 2010;
int f[M];

int main() {
    int n, m;
    cin >> n >> m;
    int v, w, s;
    for (int i = 0; i < n; i ++) {
        cin >> v >> w >> s;
        for (int k = 1; k <= s; k *= 2) {
            for (int j = m; j >= k * v; j --) {
                f[j] = max(f[j], f[j - k * v] + k * w);
            }
            s -= k;
        }
        if (s) {
            for (int j = m; j >= s * v; j --)
                f[j] = max(f[j], f[j - s * v] + s * w);
        }
    }
    cout << f[m] << endl;
    return 0;
}
  • 时间复杂度为：$O(NV)$
  • 空间复杂度为：$O(V)$

分组背包问题

问题描述

分组背包问题的描述如下：

有$N$件物品和一个容量是$V$的背包。

每组物品有若干个，同一组内的物品最多只能选一个。每件物品的体积是$v_{ij}$，价值是 $w_{ij}$，其中$i$是组号，$j$是组内编号。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式：

第一行有两个整数 $N$，$V$，用空格隔开，分别表示物品组数和背包容量。

接下来有$N$组数据：

  • 每组数据第一行有一个整数 $S_i$，表示第$i$个物品组的物品数量；
  • 每组数据接下来有$S_i$行，每行有两个整数$v_{ij}$,$w_{ij}$，用空格隔开，分别表示第$i$个物品组的第$j$个物品的体积和价值；

输出格式：

输出一个整数，表示最大价值。

数据范围：

输入样例：

1
2
3
4
5
6
7
8
3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例：

1
8

问题分析

画出思维导图如下：

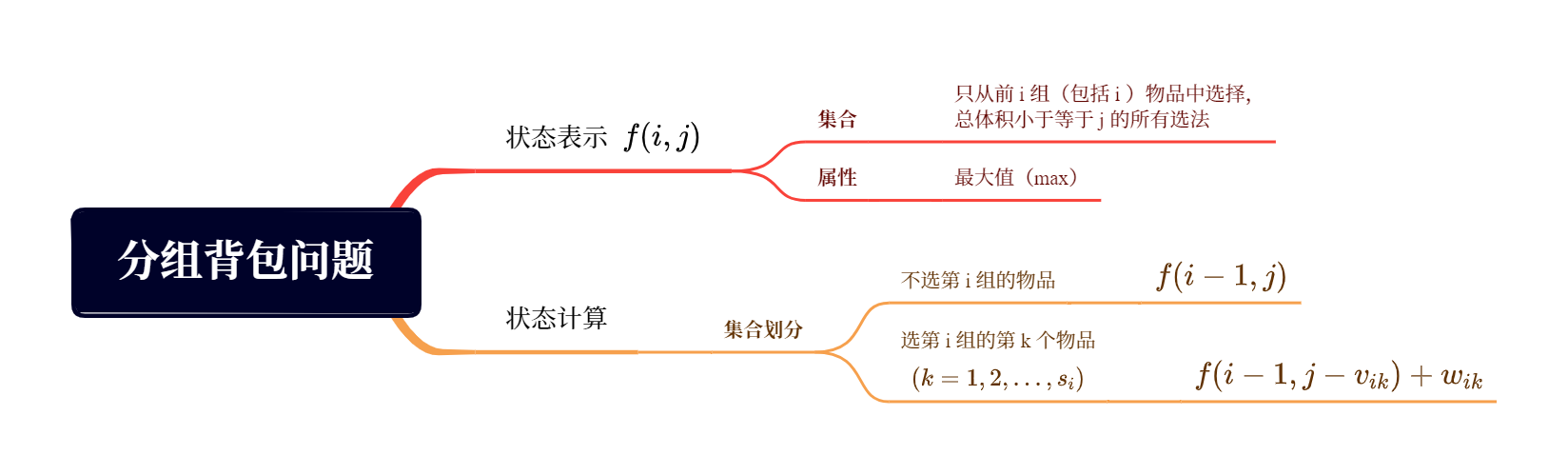
分组背包问题

状态转移方程为：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
using namespace std;

const int N = 110, M = 110, S = 110;
int f[N][M];
int s[N], v[N][S], w[N][S];

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) {
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++)
            cin >> v[i][j] >> w[i][j];
    }
    
    for (int i = 1; i <= n; i ++) {
        for (int j = 0; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            for (int k = 0; k < s[i]; k ++)
                if (j >= v[i][k])
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}
  • 时间复杂度为：$O(NVS)$
  • 空间复杂度为：$O(NV)$或$O(NS)$

代码优化

与01背包问题优化一类似，利用滚动数组减小一组存储空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
using namespace std;
const int N = 110, M = 110, S = 110;
int f[M], v[N][S], w[N][S], s[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)
    {
        scanf("%d", &s[i]);
        for (int j = 1; j <= s[i]; j ++)
            scanf("%d%d", &v[i][j], &w[i][j]);
    }
    
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= 0; j --)
            for (int k = 1; k <= s[i]; k ++)
                if (j >= v[i][k])f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    
    printf("%d", f[m]);
    return 0;
}
  • 时间复杂度为：$O(NVS)$
  • 空间复杂度为：$O(NS)$

混合背包问题

问题描述

混合背包问题的描述如下：

有$N$种物品和一个容量是$V$的背包。

物品一共有三类：

  • 第一类物品只能用1次（01背包）；
  • 第二类物品可以用无限次（完全背包）；
  • 第三类物品最多只能用$s_i$次（多重背包）；

每种体积是$v_i$，价值是$w_i$。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。

输入格式

第一行两个整数，$N$, $V$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行三个整数$v_i$，$w_i$，$s_i$，用空格隔开，分别表示第$i$种物品的体积、价值和数量。

  • $s_i$=−1表示第$i$种物品只能用1次；
  • $s_i$=0表示第$i$种物品可以用无限次；
  • $s_i$>0表示第$i$种物品可以使用$s_i$次；

输出格式

输出一个整数，表示最大价值。

数据范围

输入样例

1
2
3
4
5
4 5
1 2 -1
2 4 1
3 4 0
4 5 2

输出样例：

1
8

问题分析

对每种不同类型的物品，计算时使用不同的状态转移方程即可。注意到，01背包问题其实是多重背包问题的一种特殊情况，因此可以将它们合并进行处理。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
using namespace std;

const int N = 1010, M = 1010;
int f[M];

int main() {
    int n, m;
    cin >> n >> m;
    int v, w, s;
    for (int i = 0; i < n; i ++) {
        cin >> v >> w >> s;
        if (s == 0) {
            for (int j = v; j <= m; j ++)
                f[j] = max(f[j], f[j - v] + w);
        }
        else {
            if (s == -1) s = 1; // 若为 01 背包问题，将其转换成数量为 1 的多重背包问题
            for (int k = 1; k <= s; k *= 2) {
                for (int j = m; j >= k * v; j --) 
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            if (s) {
                for (int j = m; j >= s * v; j --)
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}
  • 最坏时间复杂度为：$O(NVS)$
  • 空间复杂度为：$O(V)$

背包问题及其优化

http://jjzhong.com/2022/11/29/背包问题及其优化/

作者

Jianjun Zhong

发布于

2022-11-29

更新于

2023-08-14

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

最新文章

标签

6.5841
6.8241
Git1
Hexo1
Icarus1
LeetCode4
Raft1
Trie1
二分查找2
二叉树1
人脸识别1
优先队列1
分布式系统1
分治1
前缀树1
动态规划3
单调栈1
双指针2
堆1
字典树1
归并排序1
数据结构1
树1
树形DP2
深度优先遍历1
深度学习1
状态机1
背包问题1
计算机视觉1
×